西瓜书绪论
解答开始
1.1 表1.1中若只包含编号1和4的两个样例,试给出相应的版本空间。

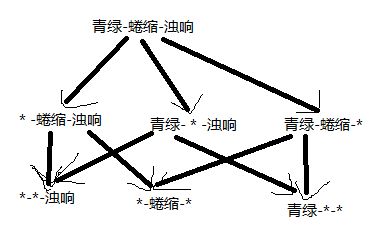
如上图所示,有7种。
1.2 与使用单个合取式来进行假设表示对比,使用“析合范式”将使得假设空间具有更强的表示能力

会把“(色泽=青绿)^(根蒂=蜷缩)^(敲声=清脆 )”以及”(色泽=乌黑)^(根蒂=硬挺)^(敲声=沉闷)”都分类为”好瓜”。若使用最多包含k个合取式的析合范式来表达表1.1西瓜分类问题的假设空间,试估算共有多少种可能的假设。

单个合取式有3(青绿、乌黑、*)× 4(蜷缩、硬挺、稍棬、*) × 4(浊响、清脆、沉闷、*) +1(空集)=49个假设空间
不考虑冗余的情况下有$\Sigma C^{k}_{49}=2^{49}$个假设空间
求法1:
以下为杨辉三角:

每一层的数字之和是一个2倍增长的数列,从第二行开始第i行第j列就是$C^{j-1}{i-1}$的值,第i行所有数的和为$2^{i-1}$,故而$\Sigma C^{k}{49}$为第50行所有数的和$2^{49}$。

求法2:
利用二项式定理
$(a+b)^n=C(n,0)a^n+C(n,1)a^{n-1}b+C(n,2)a^{n-2}b^2+C(n,n-2)a^2b^{n-2}+C(n,n-1)ab^{n-1}+C(n,n)*b^n$
再令$a=b=1$即得 $C(n,0)+C(n,1)+C(n,2)+…+C(n,n-2)+C(n,n-1)+C(n,n)=2^n$
注:杨辉三角与组合从一定意义上是互通的。
1.3 若数据集包含噪声,则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下,试设计一种归纳偏好用于假设选择。
如若数据集中有完全相同属性的两个样本出现了不同的分类标签,可以把这两个样本删除,也可以根据其他属性最接近的样本的标签决定侧重于好瓜或者侧重于坏瓜。
1.4 本章1.4节在论述没有免费的午餐定理时,默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量l,则式(1.1)将改为
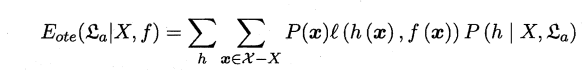
试证明“没有免费午餐定理”仍成立
以下为原来的证明:
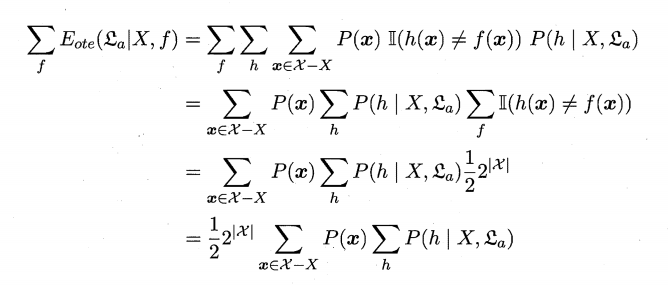
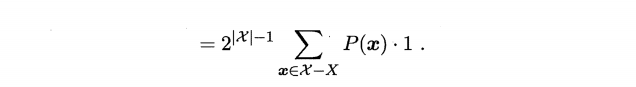
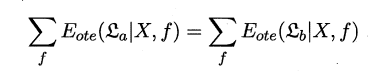
证明: