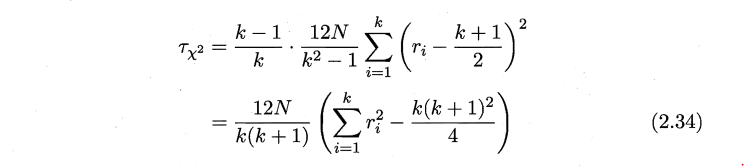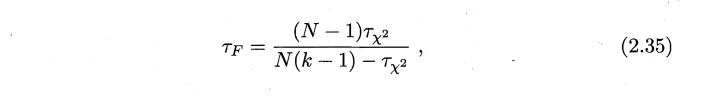2.1 数据集包含1000个样本,其中500个正例、500 个反例,将其划分为包含 70% 样本的训练集和 30% 样本的测试集用于留出法评估,试估算共有多少种划分方式.
训练集应包含350个正例和350个反例,测试集应包含150个正例和150个反例。应有
\[C^{350}_{500} \times C^{350}_{500}\]种划分方式。
2.2 数据集包含100个样本,其中正、反例各一半,假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测),试给出用10折交叉验证法和留一法分别对错误率进行评估所得的结果.
10折交叉验证时,每个训练集有45正例以及45反例。其中测试集有5正例以及5反例。训练样本正例与反例一样多故而错误率期望值应为50%。
留一法剩下的那个样本一半可能为正例,一半可能为反例。若为正例,则训练集中有49个正例与50个反例,则预测为反例,错误。若为反例,则训练集中有50个正例与49个反例,则预测为正例,错误。
2.3 若学习器A的F1值比学习器B高,试析A的BEP值是否也比B高.
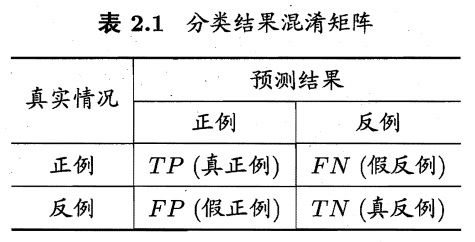
查准率
\[P = \frac{TP}{TP+FP}\]查全率
\[R = \frac{TP}{TP+FN}\]F1值
\[F1 = \frac{2\times P\times R}{P+R},\]“平衡点 (Break-Event Point,简称 BEP)是”查准率=查全率”时的取值。即P=R时的取值。
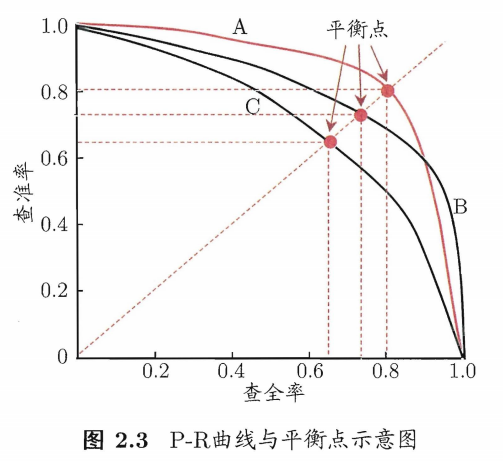
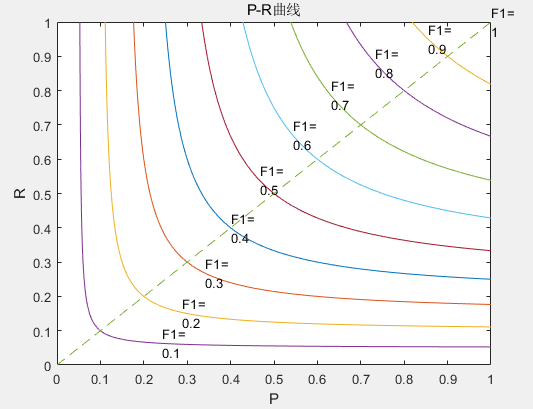
很多情形下我们可根据学习器的预测结果对样例进行排序,排在前面的是学习器认为”最可能 “是正例的样本,排在最后的则是学习器认为”最不可能”是正例的样本.按此顺序逐个把样本作为正例进行预测,则每次可以计算出当前的查全率、 查准率。以查准率为纵轴、查全率为横轴作图 ,就得到了查准率-查全率曲线,即P-R曲线。如上图。

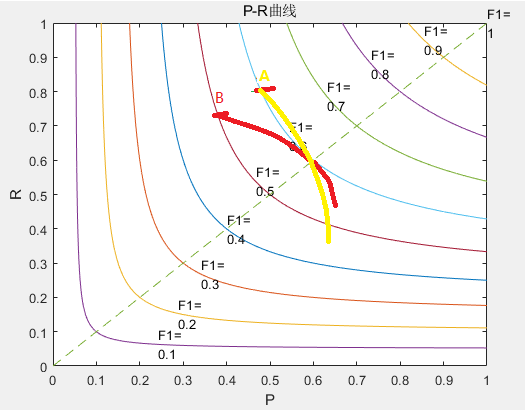
举个例子上图黄学习器在A点的F1值比红学习器的在B点的F1值高但两个学习器BEP相等。F1值随模型分类阈值的变化而变化,而BEP值只是学习器P与R相等时的值。不能仅仅因为某一个点的F1的对比而判断BEP的大小关系。
2.4 试述真正例率(TPR)、假正例率(FPR)与查准率(P)、查全率(R)之间的联系.
真正例率(TPR)
\[TPR = \frac{TP}{TP+FN}\]假正例率(FPR)
\[FPR = \frac{FP}{TN+FP}\]查准率P
\[P = \frac{TP}{TP+FP}\]查全率R
\[R = \frac{TP}{TP+FN}\]在数学关系上的转换:(TPR,FPR)->(P,R):
\[P= \frac{TPR* m_+}{TPR* m_+ +FPR* m_-} R = TPR\]在数学关系上的转换:(P,R)->(TPR,FPR):
\[TPR=R, FPR= \frac{m_+R(1-P)}{m_-P}\]其中
\[m_+ = TP+FN,m_- = FP+TN\]TPR、FPR、R的概率大小与学习器的选取有关,与测试集的正负样本的比例无关,而P的概率大小与测试集正负样本的比例有关。
2.5 试证明式(2.22).
ROC 曲线的纵轴是”真正 例率” (True Positive Rate ,简称 TPR) ,横轴是”假正例率” (False Positive Rate ,简称 FPR)。
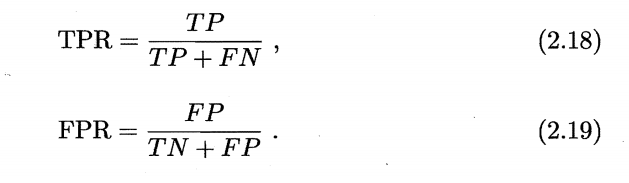
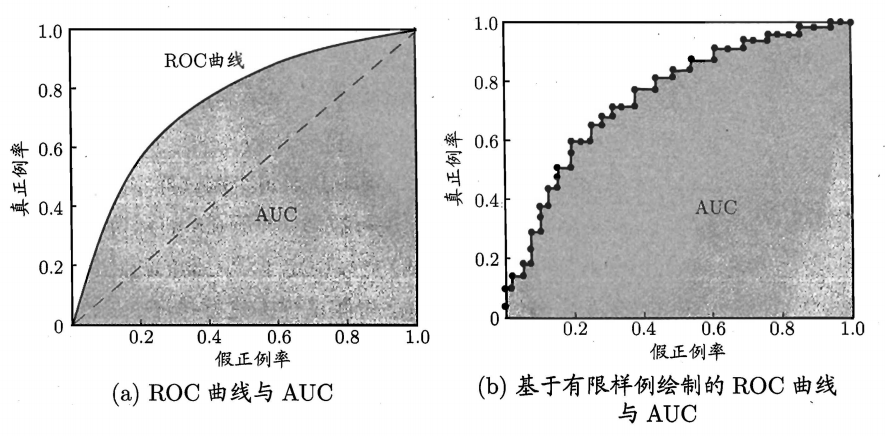
现实任务中通常是利用有限个测试样例来绘制ROC图,此时仅能获得有限个(真正例率,假正例率 )坐标对,无法产生图 2.4(a) 中的光滑 ROC 曲线 只能 绘制出如图 2.4b)所示的近似 ROC 曲线.绘图过程很简单:给定 m+ 个正例和m- 个反例,根据学习器预测结果对样例进行排序,然后把分类阈值设最大, 即把所有样例均预测为反例,此时真正例率和假正例率均为0, 在坐标(0,0) 标记一个点然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例.设前一个标记点坐标为(x,y) 当前若为真正例,则对应标记点的 坐标为(x,$y+\frac{1}{m_+}$) ;当前若为假正例,则对应标记点的坐标为 ($x+\frac{1}{m_-}$,y) ,然后用线段连接相邻点即得。
从定义可知, AUC 通过对 ROC 线下各部分的面积求和而得 ROC 曲线是由坐标为 {(X1,y1), (X2, Y2) , . . . , (Xm, Ym)} 的点按序连接而形 (X1=0, Xm = 1) 参见 2.4 (b) ,则 AUC 可估算为
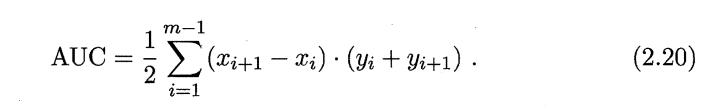
形式化地看, AUC 考虑的是样本预测的排序质量,因此它与排序误差有紧密联系.给定$m_+$ 个正例和$m_-$ 个反例,令 $D_+$和$D_-$ 分别表示正、反例集合, 则排序”损失” (loss) 定义为
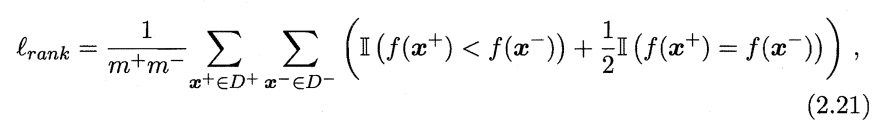

#### 易知
\[1 = \frac{1}{m_+m_-}\sum\limits_{x_+\in D_+} \sum\limits_{x_-\in D_-} (II ((f(x^+)<f(x^-))+II ((f(x^+)=f(x^-))+II ((f(x^+)>f(x^-)))\] \[1 -l_{rank}= \frac{1}{m_+m_-}\sum\limits_{x_+\in D_+} \sum\limits_{x_-\in D_-} (\frac{1}{2}II ((f(x^+)=f(x^-))+II ((f(x^+)>f(x^-)))\]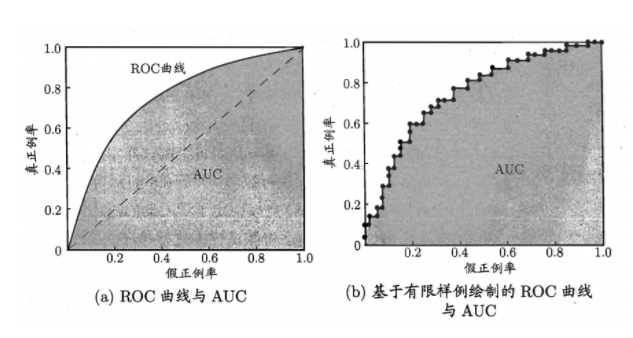
起始总和为0,把分类阈值设最大,所有样例均预测为反例,此时真正例率和假正例率均为0,越可能是正的样本排在越前面。从坐标(0,0)开始,将分类阈值按从大到小依次设为每个样例的预测值,即依次将每个样例划分为正例.设一个正样本集合D+和一个负样本集合D-,一开始两个集合都空,若下一个样本为真正例,则将该样本直接放入D+中;若下一个样本为假正例,则将该样本放入D-中并使总和加上D+集合中的样本数/m+,即为$II ((f(x^+)>f(x^-))$,表示已有若干个正例值大于此负例值,特殊地,如果有假正例与真正例相等则只加上已有相等正样本的一半。最后归一化除以m-。
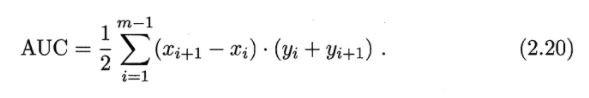
AUC与上相似的,起始总和为0,把分类阈值设最大,所有样例均预测为反例,此时真正例率和假正例率均为0,越可能是正的样本排在越前面。从(0,0)开始,若为真正例则上移1/m+,由公式可观察知AUC值不变化,若为假真例则总面积增加之前上移的次数/m+,若半真半假则总面积增加之前上移的次数+0.5/m+,最后归一化除以m-。
易分析得两者等价。

2.6 试述错误率与ROC曲线的联系.
ROC曲线上的任意一点都是对应着(FPR,TPR)

而错误率对应着$\frac{FN+FP}{m_++m_-}$
故而错误率对着每一点的不同而不同
\[\frac{(1-TPR)m_++FPRm_-}{m_++m_-}\]2.7 试证明任意一条ROC曲线都有一条代价曲线与之对应,反之亦然.
\[\frac{(1-TPR)m_++FPRm_-}{m_++m_-} = \frac{FNRm_++FPRm_-}{m_++m_-}\]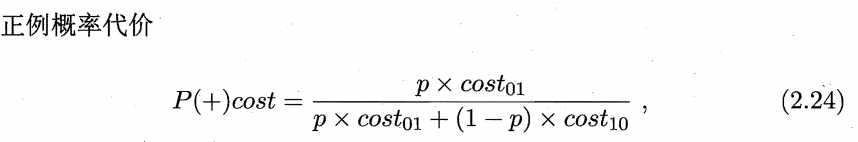
归一化代价
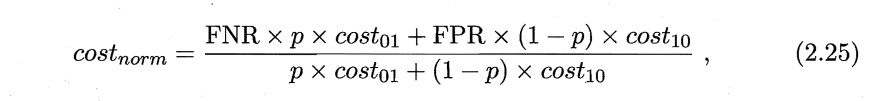
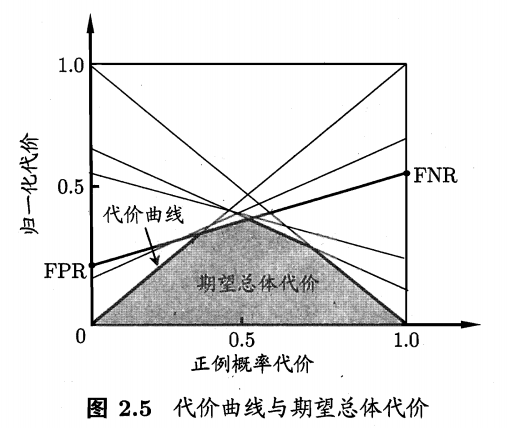
易知道
\[\begin{aligned} cost_{norm} &= FNR* P(+)cost + FPR* (1-P(+)cost) \\ & = (FNR-FPR) * P(+)cost +FPR \end{aligned}\]两者之间可以用一次函数联系起来,即两者可以互化。故而任意一条ROC曲线都有一条代价曲线与之对应,反之亦然。
2.8 Min-max 规范化和z-score 规范化是两种常用的规范化方法.令x和x’分别表示变量在规范化前后的取值,相应的,令 $x_{min}$ 和 $x_{max}$ 即表示规范化前的最小值和最大值 ,$x’{min}$ 和 $x’{max}$ 表示规范化后的最小值和最大值,$\overline{x}$ 和 $\sigma_x$ 分别表示规范化前的均值和标准差,则 min-max 规范化、 z-score 规范化分别如式(2.43)和 (2.44) 所示.试析二者的优缺点.
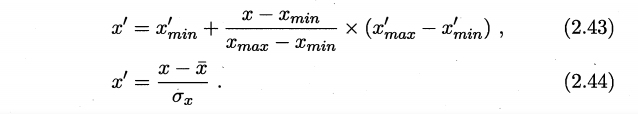
两种方式都是线性变换,数据规范化的常用方法,前者将数据转换到想要的区间之内,后者可以可以把数据调整为均值为0,标准差为1。
前者保留了原来数据中存在的关系,消除量纲与数据取值范围的影响,但是若某个单一数值很大,则规范后各个值接近于0且相差不大。
后者可以表示各个数据离均值相差多少个标准差这样的问题。z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。但是不好控制数据的范围。
2.9 试述 χ2 检验过程.
https://wiki.mbalib.com/wiki/%E5%8D%A1%E6%96%B9%E6%A3%80%E9%AA%8C
2.10* 试述在Friedman 检验中使用式(2.34) (2.35) 的区别.